Erlang: Concurrency with Sudoku

For past three decades semiconductor industry promised to double the speed of microprocessor every two years, and they did keep to their promise. Now, it looks like they have exhausted all the available tricks and the only way to increase computation speed is by going parallel - packing more number of cores in the same die. But that ain’t so easy, for it requires re-designing our algorithms to run parallel. Enter concurrent programming. Erlang is one such language that encourages concurrency.

Concurrent programming is a paradigm of writing computer programs that can execute in parallel. Three decades of structured programming concepts popularized by languages like C and Java have made the entire ecosystem of computer applications optimized for sequential programming. Now, even when we are ready to redesign our algorithms for concurrency, its implementation, testing and deployment are making life difficult for us. The general focus on Erlang here is that it may save us from some of those difficulties. Let us experiment couple of scenarios using sudoku. There is a separate article describing the algorithm and why it will make sense in this context. Source code for the same can be found in github. You can find more details on the scripts that we will using it here.

Sequential, parallel and concurrent algorithms

Sequential version of the sudoku puzzle solver is implemented as a single threaded program. An Erlang process is spawned to solve a single puzzle, which will sequentially track and back-track empty slots filling them with possible correct values. It took 6.3 ms to solve just one puzzle,

# solve a single sudoku puzzle of complexity 3 (9x9) and difficulty 40%
$ bin/sudoku -c 3 -d 40 -s 1123
complexity:3 count:1 difficulty:40 seed:1123
Time taken to evaluate 6329uS

With above parameters to sudoku script, we generated a 9x9 puzzle, populating 40% of the slots, with complexity of 3. The -s option provides seed value to the random-generator - so that same puzzles will be generated for the same seed value. To solve 100 puzzles one after another using the same erlang process, utilizing just one core, takes about 1.18 seconds.

# solve a single sudoku puzzle of complexity 3 (9x9) and difficulty 40%
$ bin/sudoku -c 3 -d 40 -s 1123 -n 100
complexity:3 count:100 difficulty:40 seed:1123
Time taken to evaluate 1182004uS

All measurements are taken with my 2GHz Core-2 Quad desktop`.

Parallel version of the sudoku puzzle solver spawns an erlang process for each puzzle and there by it can utilize all the available cores. This is not really a concurrent algorithm, but just plain vanilla parallel batch processing utilizing multiple cores. This is similar to modern web servers utilizing multiple cores.

Concurrent version of this algorithm, will spawn an erlang process for each possible path, that is, for a given empty slot if there can be 2 possible values, then two erlang process will be spawned and each one will assume one of the possible values. With this algorithm, even to solve a single puzzle, we can utilize all the available cores.

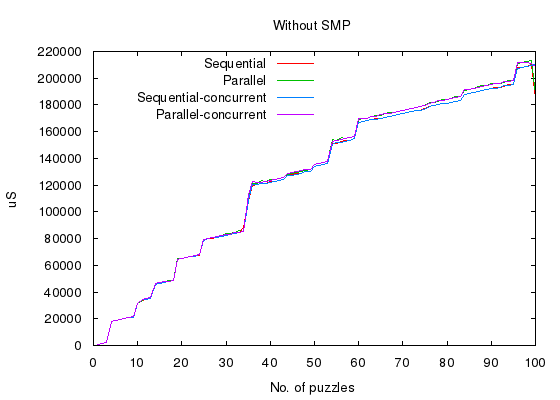
We will run the same script with few more switches, and SMP disabled.

$ bin/sudoku -c 3 -n 100 -d 40 -s 1123 -benchmark # SMP disabled

Above command generates 100 puzzles of complexity 3, 9x9 sudoku table, populating 40% of the slots. Same seed value will generate same set of tables. The script outputs five columns,

• 1st column, no.of puzzles solved.
• 2nd column time taken to solve them sequentially.
• 3rd column time taken to solve puzzles parallely, one erlang-process for each puzzle.
• 4th column same as 2nd column, except that concurrent version of algorithm is used.
• 5th column same as 3rd column, except that concurrent version of algorithm is used.

bin/sudoku was executed in SMP disabled mode by adding the following header in the beginning.

#!/usr/bin/env escript
%% -*- erlang -*-
%%! -smp disable

Let us now plot the data with gnuplot,

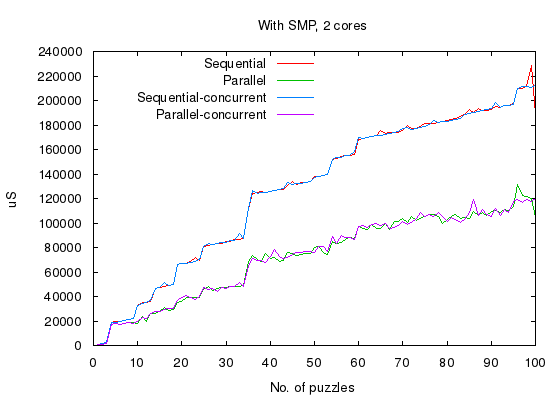
Again, the script is executed with same switches but with two cores enabled. Replace -smp disable with +S 2:2 in the script header. A similar 5-column output is generated and plotted below,

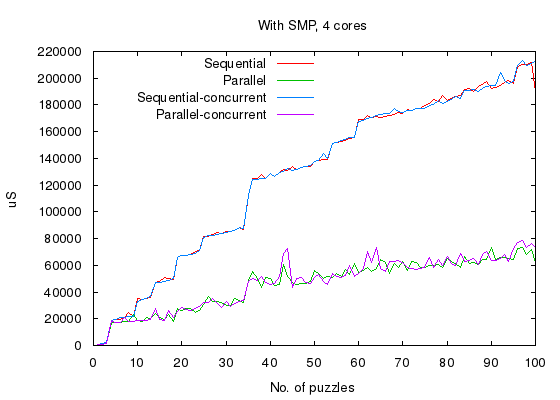
Once again, the script is executed with 4 cores enabled, that is, using the +S 4:4 switch and plotted below,

We can easily observe that,

• Whether parallel version or concurrent version, there is virtually no overhead introduced when utilizing multiple cores.
• Both parallel version and concurrent version can linearly scale with number of cores.

Parallel version is plotted on single-core, 2-core, and 4-core variants,

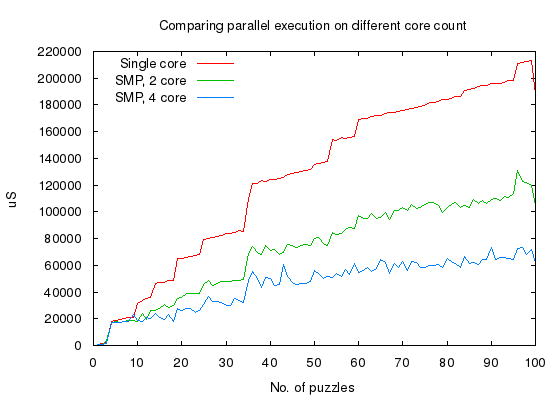
We can observe that parallel version scales linearly with number of cores.

Concurrent version, when executed one after another using the same erlang process, is plotted on single-core, 2-core, and 4-core variants,

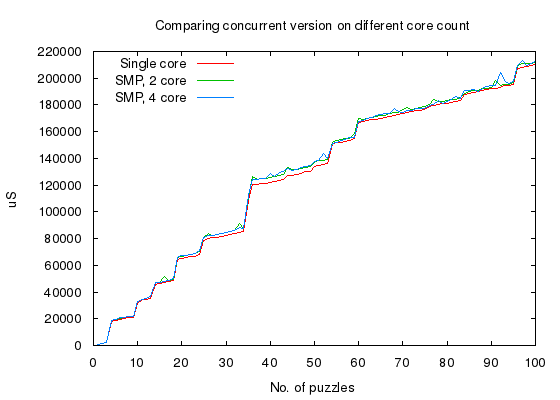
Shows that there is no improvement of using a concurrent version of the algorithm and neither a overhead of using it.

Performance for pathological cases ?

Let us apply sequential version and concurrent version of the algorithm for a pathological sudoku combination and measure its performance on different core-counts. A puzzle can be pathological when it leads the algorithm to backrack millions or billions of time before it end up on the right path.

I have added two puzzle files priv/long3.term and long4.term, both having a pathological case.

First we will solve the pathological case with sequential version,

$ bin/sudoku -f priv/long3.term         # SMP disabled
Time taken to evaluate: 3988177uS       # 3.9 Seconds

Then with concurrent version, on different number of cores.

$ bin/sudoku -t -f priv/long3.term      # SMP with 4 cores
Time taken to evaluate: 195572uS        # 195 milliseconds

$ bin/sudoku -t -f priv/long3.term      # SMP with 2 cores
Time taken to evaluate: 415335uS        # 415 milliseconds

$ bin/sudoku -t -f priv/long3.term      # SMP disabled
Time taken to evaluate: 1078302uS       # 1 second

-t switch enables the concurrent mode, we can see that between 4 cores and 2 cores there is 2x improvement because the concurrent logic is making use of the extra cores. But what will surprise us is that,

concurrent version performs 4x better even on a single-core. And with 4 cores, performance improves to 20x. How does that happen ? welcome to swarm algorithms !!

Swarm algorithm

A backtracking algorithm becomes a swarm algorithm when it explores as many path as possible simultaneously, thus it avoids spending time on bad bath. In many cases the number of steps in a backtracking algorithm is not more than couple of hundred, and we find that, given enough execution time for the good path it gets completed quick enough. Note that swarm algorithm does not remove the exponential complexity of backtracking logic - but it gives a great deal on performance.

This experiment might also teach us that concurrent programming is not just about multiple cores.

Long ago, I wrote a similar Sudoku puzzle solver in C / Linux, but the best part of writing it in Erlang is the way it prompted me to re-design the algorithm for concurrency. In C, I would have never thought of spawning a new process for every choice it makes, but here it was only natural.

That is how a language can affect our creativity, be it for programming or for poetry. And it is those simple and unassuming things that changes one’s perspective.